Review a colleague's paragraph.
With the same partner each of you discuss the pro-con issue addressed.
Premise
https://m.youtube.com/watch?v=jzmZhJmHMsw
For Discussion today find a partner who wrote a paragraph on a different selection from Part 2 of the textbook that you did not work on. With your partner explain the selection that you were assigned to answer.
Kindly bring a hard copy of your Pro-Con paper to class on Wednesday.
Learning objective: explain premise in your own words and provide an example. Explain inductive and deductive reasoning and provide examples.
Explain your assigned question selection from Part 2 and one other question from Part 2 of the textbook.
If during the semester you have an example of how your six top values aided you personally or professionally let me know. I would like to hear about your experience.
Discussion: Refer to the six top values that you identified in our previous discussion.
In groups of four answer:
1. Am I living my life today in alignment with my values?
2. Am I interacting with others today in alignment with my values?
3. Am I prioritizing and making decisions today in alignment with my values?
Wednesday assignment: type a paragraph to be collected with your name on it and bring to class the next time we meet.
In groups of four each person in the group will type a paragraph answering one of the #1-4 questions for the assigned selection in Part 2. Each group of four students can self-assign which of the #1-4 questions they will answer for the assigned selection in Part 2.
I will assign each group a selection from Part 2 to answer.
Learning objectives: one, find a partner whose name you do not know so you learn another colleague's name. Two, this person must not have addressed the same selection or question that you wrote about so you learn something about another selection in Part 2. Three, review whether the person followed the directions of the assignment: is the assignment typed? Did the person write one paragraph?
Perhaps most importantly, read your colleague's paragraph but do not have your colleague explain anything about their paragraph. Read it silently. With your editor's pen in hand comment on the mechanics of the selection and note, by writing on your colleague's paper, any questions that you have.
After you have written corrections, comments, and made notes on their paragraph feel free to discuss their answer.
Next, we will review the first written assignment (Pro-Con argument) which is due Wednesday.
Part 2: Reasoning
Logic Logic (from the Ancient Greek: λογική, logikḗ), originally meaning "the word" or "what is spoken" (but coming to mean "thought" or "reason"), is generally held to consist of the systematic study of the form of arguments. A valid argument is one where there is a specific relation of logical support between the assumptions of the argument and its conclusion. (In ordinary discourse, the conclusion of such an argument may be signified by words like therefore, hence, ergo and so on.)
There is no universal agreement as to the exact scope and subject matter of logic, but it has traditionally included the classification of arguments, the systematic exposition of the 'logical form' common to all valid arguments, the study of inference, including fallacies, and the study of semantics, including paradoxes. Historically, logic has been studied in philosophy (since ancient times) and mathematics (since the mid-1800s), and recently logic has been studied in computer science, linguistics, psychology, and other fields.
What is Logic? (Philosophical Definition), 5:51
A definition of Logic as a field of philosophy, as well as several types of logic studied in philosophy, including second order logic, non-classical Logic, and modal logic.
https://youtu.be/ZPfw422Wcso
premise
A premise or premiss[a] is a statement that an argument claims will induce or justify a conclusion. In other words, a premise is an assumption that something is true. In logic, an argument requires a set of (at least) two declarative sentences (or "propositions") known as the premises or premisses along with another declarative sentence (or "proposition") known as the conclusion. This structure of two premises and one conclusion forms the basic argumentative structure. More complex arguments can use a series of rules to connect several premises to one conclusion, or to derive a number of conclusions from the original premises which then act as premises for additional conclusions. An example of this is the use of the rules of inference found within symbolic logic.
Aristotle held that any logical argument could be reduced to two premises and a conclusion. Premises are sometimes left unstated in which case they are called missing premises, for example:
Socrates is mortal because all men are mortal.
It is evident that a tacitly understood claim is that Socrates is a man. The fully expressed reasoning is thus:
Because all men are mortal and Socrates is a man, Socrates is mortal.
In this example, the independent clauses preceding the comma (namely, "all men are mortal" and "Socrates is a man") are the premises, while "Socrates is mortal" is the conclusion.
The proof of a conclusion depends on both the truth of the premises and the validity of the argument.
Identifying Premises and Conclusions, 5:34
Before you can analyze an argument you need to be sure that you've clearly identified the conclusion and the premises. This video discusses some of the challenges associated with this task.
https://youtu.be/07mehbgE5jc
deductive-inductive
Inductive reasoning (as opposed to deductive reasoning or abductive reasoning) is reasoning in which the premises are viewed as supplying strong evidence for the truth of the conclusion. While the conclusion of a deductive argument is certain, the truth of the conclusion of an inductive argument may be probable, based upon the evidence given.
Many dictionaries define inductive reasoning as the derivation of general principles from specific observations, though some sources disagree with this usage.
The philosophical definition of inductive reasoning is more nuanced than simple progression from particular/individual instances to broader generalizations. Rather, the premises of an inductive logical argument indicate some degree of support (inductive probability) for the conclusion but do not entail it; that is, they suggest truth but do not ensure it. In this manner, there is the possibility of moving from general statements to individual instances (for example, statistical syllogisms, discussed below).
What is an Inductive Argument? 1:41
In this video we introduce the concept of an "inductive argument" as this term is commonly used in logic and philosophy (see my other video on "Induction and Science" for a discussion of how scientists commonly use the term, and it compares with the usage given here).
https://youtu.be/affFHkV4kNo
Inductive reasoning (as opposed to deductive reasoning or abductive reasoning) is reasoning in which the premises are viewed as supplying strong evidence for the truth of the conclusion. While the conclusion of a deductive argument is certain, the truth of the conclusion of an inductive argument may be probable, based upon the evidence given.
Many dictionaries define inductive reasoning as the derivation of general principles from specific observations, though some sources disagree with this usage.
The philosophical definition of inductive reasoning is more nuanced than simple progression from particular/individual instances to broader generalizations. Rather, the premises of an inductive logical argument indicate some degree of support (inductive probability) for the conclusion but do not entail it; that is, they suggest truth but do not ensure it. In this manner, there is the possibility of moving from general statements to individual instances (for example, statistical syllogisms, discussed below).
What is an Inductive Argument? 1:41
In this video we introduce the concept of an "inductive argument" as this term is commonly used in logic and philosophy (see my other video on "Induction and Science" for a discussion of how scientists commonly use the term, and it compares with the usage given here).
https://youtu.be/affFHkV4kNo
Deductive reasoning, also deductive logic, logical deduction is the process of reasoning from one or more statements (premises) to reach a logically certain conclusion. It differs from inductive reasoning.
Deductive reasoning links premises with conclusions. If all premises are true, the terms are clear, and the rules of deductive logic are followed, then the conclusion reached is necessarily true.
Deductive reasoning (top-down logic) contrasts with inductive reasoning (bottom-up logic) in the following way: In deductive reasoning, a conclusion is reached reductively by applying general rules that hold over the entirety of a closed domain of discourse, narrowing the range under consideration until only the conclusion(s) is left. In inductive reasoning, the conclusion is reached by generalizing or extrapolating from specific cases to general rules, i.e., there is epistemic uncertainty. However, the inductive reasoning mentioned here is not the same as induction used in mathematical proofs – mathematical induction is actually a form of deductive reasoning.
What is a Deductive Argument? 2:18
This video introduces the concept of a "deductive argument" and how it relates to the logical concept of "validity".
https://youtu.be/oGNnzfsfUAs
Deductive reasoning links premises with conclusions. If all premises are true, the terms are clear, and the rules of deductive logic are followed, then the conclusion reached is necessarily true.
Deductive reasoning (top-down logic) contrasts with inductive reasoning (bottom-up logic) in the following way: In deductive reasoning, a conclusion is reached reductively by applying general rules that hold over the entirety of a closed domain of discourse, narrowing the range under consideration until only the conclusion(s) is left. In inductive reasoning, the conclusion is reached by generalizing or extrapolating from specific cases to general rules, i.e., there is epistemic uncertainty. However, the inductive reasoning mentioned here is not the same as induction used in mathematical proofs – mathematical induction is actually a form of deductive reasoning.
What is a Deductive Argument? 2:18
This video introduces the concept of a "deductive argument" and how it relates to the logical concept of "validity".
https://youtu.be/oGNnzfsfUAs
Ninety Second Philosophy: Deductive vs Inductive Arguments, 1:32
A quick video explaining the difference between deductive and inductive arguments.
Information for this video gathered from The Stanford Encyclopedia of Philosophy, The Internet Encyclopedia of Philosophy, The Cambridge Dictionary of Philosophy, The Oxford Dictionary of Philosophy and more!
A quick video explaining the difference between deductive and inductive arguments.
Information for this video gathered from The Stanford Encyclopedia of Philosophy, The Internet Encyclopedia of Philosophy, The Cambridge Dictionary of Philosophy, The Oxford Dictionary of Philosophy and more!
fallacies: petitio principii (begging the question)
To beg the question is to assume the truth of the conclusion of an argument in the premises in order for the conclusion to follow. One of the simplest examples is the claim, "Paranormal activity is real because I have experienced what can only be described as paranormal activity." In this example, the conclusion "Paranormal activity is real" is assumed to be true when the person argues that they have experienced what can only be described as paranormal activity. Thus, the conclusion is assumed to be true in the premise. If a person does not assume that "Paranormal activity is real" is true in the premise, as that is exactly what must be established, then the conclusion does not follow. It is a type of circular reasoning and an informal fallacy, in which an arguer makes an argument that requires the desired conclusion to be true. This often occurs in an indirect way such that the fallacy's presence is hidden or at least not easily apparent.
The term "begging the question", as it is usually phrased, originated in the 16th century as a mistranslation of the Latin petitio principii, which actually translates to "assuming the initial point". In modern vernacular usage, "to beg the question" frequently appears to mean "to raise the question" (as in, "This begs the question, whether...") or "to dodge a question". In contexts that demand strict adherence to a technical definition of the term, many consider these usages incorrect.
p. 53
"We must not drink liquor."
Why do you say that?
Drinking is against the will of Allah.
How do you know?
The Koran says so.
But how do you know the Koran is right?
Everything said in the Koran is right.
How do you know that?
Why, it's all divinely inspired.
But how do you know that?
Why, the Koran itself declares that it is divinely inspired.
But why believe that?
You've got to believe the Koran, because everything in the Koran is right."
This chain of reasoning is a more extended case of begging the question; the speaker is reasoning in a large circle, taking for granted one of the things that is supposed to be be proved
Are you Begging the Question? - Gentleman Thinker, 1:43
A common philosophical mistake! Have you told somebody that they've begged the question? Did you use the term correctly? Gentleman Thinker playlist: https://www.youtube.com/watch?v=94YV6...
https://youtu.be/OAXKc-rvMa8
To beg the question is to assume the truth of the conclusion of an argument in the premises in order for the conclusion to follow. One of the simplest examples is the claim, "Paranormal activity is real because I have experienced what can only be described as paranormal activity." In this example, the conclusion "Paranormal activity is real" is assumed to be true when the person argues that they have experienced what can only be described as paranormal activity. Thus, the conclusion is assumed to be true in the premise. If a person does not assume that "Paranormal activity is real" is true in the premise, as that is exactly what must be established, then the conclusion does not follow. It is a type of circular reasoning and an informal fallacy, in which an arguer makes an argument that requires the desired conclusion to be true. This often occurs in an indirect way such that the fallacy's presence is hidden or at least not easily apparent.
The term "begging the question", as it is usually phrased, originated in the 16th century as a mistranslation of the Latin petitio principii, which actually translates to "assuming the initial point". In modern vernacular usage, "to beg the question" frequently appears to mean "to raise the question" (as in, "This begs the question, whether...") or "to dodge a question". In contexts that demand strict adherence to a technical definition of the term, many consider these usages incorrect.
p. 53
"We must not drink liquor."
Why do you say that?
Drinking is against the will of Allah.
How do you know?
The Koran says so.
But how do you know the Koran is right?
Everything said in the Koran is right.
How do you know that?
Why, it's all divinely inspired.
But how do you know that?
Why, the Koran itself declares that it is divinely inspired.
But why believe that?
You've got to believe the Koran, because everything in the Koran is right."
This chain of reasoning is a more extended case of begging the question; the speaker is reasoning in a large circle, taking for granted one of the things that is supposed to be be proved
Are you Begging the Question? - Gentleman Thinker, 1:43
A common philosophical mistake! Have you told somebody that they've begged the question? Did you use the term correctly? Gentleman Thinker playlist: https://www.youtube.com/watch?v=94YV6...
https://youtu.be/OAXKc-rvMa8
complex question
Complex Question (Logical Fallacy), 1:37
A short explanation of the Logical Fallacy of Complex Question (Fallacy February & 90 Second Philosophy)
https://youtu.be/BRflpIUqYiI
Complex Question (Logical Fallacy), 1:37
A short explanation of the Logical Fallacy of Complex Question (Fallacy February & 90 Second Philosophy)
https://youtu.be/BRflpIUqYiI
ad hominem
Ad hominem (Latin for "to the man" or "to the person"), short for argumentum ad hominem, is where an argument is rebutted by attacking the character, motive, or other attribute of the person making the argument, or persons associated with the argument, rather than attacking the substance of the argument itself.
However, its original meaning was an argument "calculated to appeal to the person addressed more than to impartial reason".
Fallacious ad hominem reasoning is normally categorized as an informal fallacy, more precisely as a genetic fallacy, a subcategory of fallacies of irrelevance.
However, in some cases, ad hominem attacks can be non-fallacious; i.e., if the attack on the character of the person is directly tackling the argument itself. For example, if the truth of the argument relies on the truthfulness of the person making the argument—rather than known facts—then pointing out that the person has previously lied is not a fallacious argument.
The Ad Hominem Fallacy | Idea Channel | PBS Digital Studios, 2:22
https://youtu.be/IVFK8sVdJNg
Ad hominem (Latin for "to the man" or "to the person"), short for argumentum ad hominem, is where an argument is rebutted by attacking the character, motive, or other attribute of the person making the argument, or persons associated with the argument, rather than attacking the substance of the argument itself.
However, its original meaning was an argument "calculated to appeal to the person addressed more than to impartial reason".
Fallacious ad hominem reasoning is normally categorized as an informal fallacy, more precisely as a genetic fallacy, a subcategory of fallacies of irrelevance.
However, in some cases, ad hominem attacks can be non-fallacious; i.e., if the attack on the character of the person is directly tackling the argument itself. For example, if the truth of the argument relies on the truthfulness of the person making the argument—rather than known facts—then pointing out that the person has previously lied is not a fallacious argument.
The Ad Hominem Fallacy | Idea Channel | PBS Digital Studios, 2:22
https://youtu.be/IVFK8sVdJNg
black and white thinking (either-or fallacy).
A false dilemma is a type of informal fallacy in which something is falsely claimed to be an "either/or" situation, when in fact there is at least one additional option.
The options may be a position that is between two extremes (such as when there are shades of grey) or may be completely different alternatives. Phrasing that implies two options (dilemma, dichotomy, black-and-white) may be replaced with other number-based nouns, such as a "false trilemma", "false tetralemma", or "false pentalemma" ("false trichotomy," "false tetrachotomy", "false pentachotomy", etc.) if something is reduced to only three, four, or five options.
A false dilemma can arise intentionally, when a fallacy is used in an attempt to force a choice or outcome. The opposite of this fallacy is false compromise.
The false dilemma fallacy can also arise simply by accidental omission of additional options rather than by deliberate deception. For example "Stacey spoke out against capitalism, therefore she must be a communist" (she may be neither). "Roger opposed an atheist argument against Christianity, but he would say that, he's a Christian" (When it's assumed the opposition by itself means he's a Christian). Roger might be an atheist who disagrees with the logic of some particular argument against Christianity. Additionally, it can be the result of habitual tendency, whatever the cause, to view the world with limited sets of options.
Some philosophers and scholars believe that "unless a distinction can be made rigorous and precise it isn't really a distinction". An exception is analytic philosopher John Searle, who called it an incorrect assumption that produces false dichotomies. Searle insists that "it is a condition of the adequacy of a precise theory of an indeterminate phenomenon that it should precisely characterize that phenomenon as indeterminate; and a distinction is no less a distinction for allowing for a family of related, marginal, diverging cases." Similarly, when two options are presented, they often are, although not always, two extreme points on some spectrum of possibilities; this may lend credence to the larger argument by giving the impression that the options are mutually exclusive of each other, even though they need not be. Furthermore, the options in false dichotomies typically are presented as being collectively exhaustive, in which case the fallacy may be overcome, or at least weakened, by considering other possibilities, or perhaps by considering a whole spectrum of possibilities, as in fuzzy logic.
The Black and White Fallacy | Idea Channel | PBS Digital Studios, 2:04
https://youtu.be/eqz53d-fYL8
A false dilemma is a type of informal fallacy in which something is falsely claimed to be an "either/or" situation, when in fact there is at least one additional option.
The options may be a position that is between two extremes (such as when there are shades of grey) or may be completely different alternatives. Phrasing that implies two options (dilemma, dichotomy, black-and-white) may be replaced with other number-based nouns, such as a "false trilemma", "false tetralemma", or "false pentalemma" ("false trichotomy," "false tetrachotomy", "false pentachotomy", etc.) if something is reduced to only three, four, or five options.
A false dilemma can arise intentionally, when a fallacy is used in an attempt to force a choice or outcome. The opposite of this fallacy is false compromise.
The false dilemma fallacy can also arise simply by accidental omission of additional options rather than by deliberate deception. For example "Stacey spoke out against capitalism, therefore she must be a communist" (she may be neither). "Roger opposed an atheist argument against Christianity, but he would say that, he's a Christian" (When it's assumed the opposition by itself means he's a Christian). Roger might be an atheist who disagrees with the logic of some particular argument against Christianity. Additionally, it can be the result of habitual tendency, whatever the cause, to view the world with limited sets of options.
Some philosophers and scholars believe that "unless a distinction can be made rigorous and precise it isn't really a distinction". An exception is analytic philosopher John Searle, who called it an incorrect assumption that produces false dichotomies. Searle insists that "it is a condition of the adequacy of a precise theory of an indeterminate phenomenon that it should precisely characterize that phenomenon as indeterminate; and a distinction is no less a distinction for allowing for a family of related, marginal, diverging cases." Similarly, when two options are presented, they often are, although not always, two extreme points on some spectrum of possibilities; this may lend credence to the larger argument by giving the impression that the options are mutually exclusive of each other, even though they need not be. Furthermore, the options in false dichotomies typically are presented as being collectively exhaustive, in which case the fallacy may be overcome, or at least weakened, by considering other possibilities, or perhaps by considering a whole spectrum of possibilities, as in fuzzy logic.
The Black and White Fallacy | Idea Channel | PBS Digital Studios, 2:04
https://youtu.be/eqz53d-fYL8
False Dilemma, :24
A false dilemma fallacy on the TV show According to Jim.
https://youtu.be/Dln3DJEcghY
A false dilemma fallacy on the TV show According to Jim.
https://youtu.be/Dln3DJEcghY
Orange Slice commercial 1988 "You either got it, or you don't!" :29
Orange Slice commercial from 1988. I ripped this from an old VHS tape I have, and did the best with the quality that I could.
https://youtu.be/mkULHzFpvmw
Necessary and sufficient conditions.
In logic, necessity and sufficiency are implicational relationships between statements.
The assertion that one statement is a necessary and sufficient condition of another means that the former statement is true if and only if the latter is true. That is, the two statements must be either simultaneously true or simultaneously false.
CRITICAL THINKING - Fundamentals: Necessary and Sufficient Conditions [HD], 3:14
In this video, Kelley Schiffman (Yale University) discusses one of the most basic tools in the philosophers's tool kit: the distinction between necessary and sufficient conditions. Through the use of ordinary language glosses and plenty of examples this mighty distinction is brought down to earth and presented in a ready-to-use fashion.
https://youtu.be/5LqNm9d2__I
Orange Slice commercial from 1988. I ripped this from an old VHS tape I have, and did the best with the quality that I could.
https://youtu.be/mkULHzFpvmw
Necessary and sufficient conditions.
In logic, necessity and sufficiency are implicational relationships between statements.
The assertion that one statement is a necessary and sufficient condition of another means that the former statement is true if and only if the latter is true. That is, the two statements must be either simultaneously true or simultaneously false.
CRITICAL THINKING - Fundamentals: Necessary and Sufficient Conditions [HD], 3:14
In this video, Kelley Schiffman (Yale University) discusses one of the most basic tools in the philosophers's tool kit: the distinction between necessary and sufficient conditions. Through the use of ordinary language glosses and plenty of examples this mighty distinction is brought down to earth and presented in a ready-to-use fashion.
https://youtu.be/5LqNm9d2__I
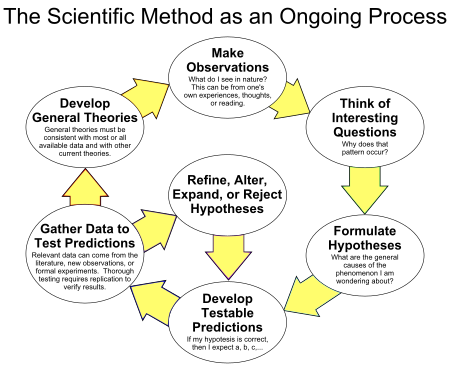
Scientific method
The Big Bang Theory Scientific Method Clip Season 6 Episode 5, :53
https://youtu.be/_7sSuhQ1_24
Scientific Method Monty Python, 5:27
https://youtu.be/k2MhMsLn9B0
Straw Man Fallacy, 2:11
https://m.youtube.com/watch?v=cGZkCPo7tC0

The Big Bang Theory Scientific Method Clip Season 6 Episode 5, :53
https://youtu.be/_7sSuhQ1_24
Scientific Method Monty Python, 5:27
https://youtu.be/k2MhMsLn9B0
Straw Man Fallacy, 2:11
https://m.youtube.com/watch?v=cGZkCPo7tC0
The Scope of Logic
Wesley C. Salmon
Wesley C. Salmon
Improving Your Thinking
Stephen F. Barker
Stephen F. Barker
Necessary and Sufficient Conditions
Steven M. Cahn
Steven M. Cahn
Thinking to Some Purpose
L. Susan Stebbing
L. Susan Stebbing
Pushover Arguments
Scott F. Aikin and Robert B. Talisse
Scott F. Aikin and Robert B. Talisse
Fixing Belief
Morris R. Cohen and Ernest Nagel
Morris R. Cohen and Ernest Nagel
Scientific Inquiry
Carl G. Hempel
Carl G. Hempel
Antiscientism
Gillian Barker and Philip Kitcher
Gillian Barker and Philip Kitcher
